Главная Экономика Книги Моделювання економіки - Вітлінський В.В.

Моделювання економіки - Вітлінський В.В.

3.2.2. Моделювання випадкових подій

Моделювання випадкових подій полягає у відтворенні факту появи чи непояви випадкової події відповідно до заданої ймовірності. Моделювання повної групи несумісних подій А1, А2, …, Аn, імовірності котрих P(Ai) = pi, i = 1, …, n відомі, можна привести до моделювання дискретної випадкової величини Y, яка має закон розподілу P(yi) = pi, де ймовірність її можливих значень

P(yi) = P(Ai) = pi.

Тобто прийняття дискретною випадковою величиною Y можливого значення yі еквівалентне появі події Аі. Для практичної реалізації даного способу спочатку на одиничному відрізку числової осі відкладають інтервали Di = pi.

Генерують рівномірно розподілену на інтервалі (0; 1) випадкову величину, реалізацією котрої є випадкове число xj, і перевіряють умову:

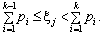(3.7)

При виконанні умови (3.7) вважають, що за цього випробування відбулася подія Аk.

Приклад. Імовірність появи події А у кожному випробуванні дорівнює Р(А) = 0,75. Необхідно змоделювати три випробування і визначити послідовність реалізації події А.

Розв’язання. Відкладемо на одиничному відрізку числової осі точку Е = 0,75 і вважатимемо, що коли випадкове число xі < E, то у випробуванні настала подія А. У протилежному випадку (при 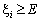) настала подія не А (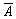), тобто подія А не мала місця.

Припустимо, наприклад, що з відповідної таблиці обрані випадкові числа x1 = 0,925, x2 = 0,135, x3 = 0,088. Тоді за трьох випробувань отримаємо таку послідовність реалізації подій: 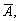А, А.

Моделювання сумісних (залежних і незалежних) подій можна виконати двома способами.

Перший спосіб. На першому етапі моделювання визначають усі можливі варіанти появи сумісних подій у випробуванні. Знаходять повну групу несумісних подій та обчислюють їх імовірності.

На другому етапі вчиняють так само, як і в моделюванні повної групи несумісних подій.

Приклад. Нехай при випробуванні мають місце залежні й су- місні події А та В, при цьому відомо, що Р(А) = 0,7; Р(В) = 0,5; Р(АВ) = 0,3.

Потрібно змоделювати появу подій А та В у двох випробуваннях.

Розв’язання. У кожному випробуванні можливі чотири несумісних результати, тобто настання чотирьох подій:

• С1 = АВ, Р(С1) = Р(АВ) = 0,3.
• С2 =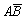, Р(С2) = Р(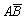) = Р(А) – Р(ВА) = 0,7 – 0,3 = 0,4.
• С3 =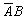, Р(С3) = Р(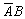) = Р(В) – Р(АВ) = 0,5 – 0,3 = 0,2.
• С4 =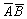, Р(С4) = 1 – [Р(С1) + Р(С2) + Р(С3)] = 1 – (0,3 + 0,4 + + 0,2) = 0,1.

Змоделюймо повну групу подій С1, С2, С3, С4 у двох випробуваннях (прогонах). Попередньо на одиничному відрізку числової осі (рис. 3.1) послідовно відкладемо інтервали:

Dі = Р(Сі), і = 1,…, 4.

Рис. 3.1. Інтервали Dі = Р(Сі)

Нехай отримано (взято з відповідної таблиці) випадкові числа x1 = 0,68 і x2 = 0,95.

Випадкове число x1 належить до інтервалу D2, тому при першому випробуванні мала місце подія А, а подія В не настала. За другого випробування випадкове число x2 належить до інтервалу D4. Обидві події А та В не мали місця.

Другий спосіб. Моделювання сумісних подій полягає у розігруванні факту появи кожної із сумісних подій окремо, при цьому, якщо події залежні, треба попередньо визначити умовні ймовірності.

Приклад. Використовуючи умови попереднього прикладу, потрібно змоделювати окрему появу подій А та В в одному випробуванні.

Розв’язання. Події А та В є залежними, тому попередньо знаходимо умовні ймовірності Р(В/А) та Р():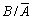

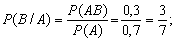
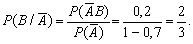
Для моделювання події А обрано випадкове число x1. Нехай x1 = 0,96. Оскільки x1>P(A), то подія А у випробуванні не настала.

Тепер розіграємо подію В за умови, що подія А у випробуванні не мала місця. Нехай випадкове число x2 = 0,22. Отже, 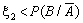(0,22 < 2/3), тобто маємо, що подія В за випробування настала.