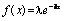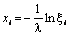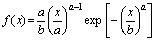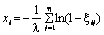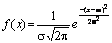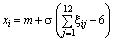- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Экономика Экономика  Книги Книги  Моделювання економіки - Вітлінський В.В. Моделювання економіки - Вітлінський В.В. |
Моделювання економіки - Вітлінський В.В.
3.2.1. Моделювання випадкових величин
Для моделювання випадкової величини потрібно знати закон її розподілу. Найзагальнішим способом отримання послідовності випадкових чисел, що є послідовністю реалізацій випадкової величини, котра розподілена за довільним законом, є спосіб, в основі якого — процес формування їх з вихідної послідовності випадкових чисел. Ця послідовність є послідовністю реалізацій випадкової величини, що розподілена в інтервалі (0; 1) згідно з рівномірним законом розподілу.
Згадану послідовність випадкових чисел з рівномірним законом розподілу можна отримати трьома способами:
- використанням таблиць випадкових чисел;
- застосуванням генераторів випадкових чисел;
- методом псевдовипадкових чисел.
Нині використовують псевдовипадкові числа, що відповідають рівномірному закону розподілу. Псевдовипадкові (випадкові) числа— це числа, отримані за деяким правилом (формулою), що імітує значення випадкової величини. Розроблено низку алгоритмів для отримання псевдовипадкових чисел. Датчики псевдовипадкових чисел є складовими більшості програмних комплексів.
Для перетворення послідовності випадкових чисел, що є реалізаціями випадкової величини з рівномірним законом розподілу в інтервалі (0; 1), у послідовність випадкових чисел, що є реалізаціями випадкової величини із заданою інтегральною функцією розподілу F(x), треба із сукупності випадкових чисел з рівномірним законом розподілу в інтервалі (0; 1) вибрати випадкове число ? і розв’язати рівняння:
F(x) = x відносно 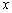 . (3.5)
. (3.5)
У випадку, коли задана функція щільності ймовірності f(x), співвідношення (3.5) набирає вигляду:
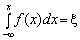 . (3.6)
. (3.6)
Для низки законів розподілу отримано аналітичний розв’язок рівняння (3.6), результат якого наведено в таблиці 3.1.
Таблиця 3.1
Формули для моделювання випадкових величин
Закони розподілу випадкової величини | Щільність розподілу | Формули для моделювання випадкових величин |
Експоненційний |
|
|
Вейбула |
|
|
Гама-розподіл (? — цілі числа) |
|
|
Нормальний |
|
|
Created/Updated: 25.05.2018
 |
|