- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Экономика Экономика  Книги Книги  Моделювання економіки - Вітлінський В.В. Моделювання економіки - Вітлінський В.В. |
Моделювання економіки - Вітлінський В.В.
16.3. Умова арбітражу та ефективний ринок
У теоретичних дослідженнях буває зручнішим користуватися не дискретними, а неперервними моделями, котрі, як правило, є менш громіздкими. Для неперервного детермінованого процесу зміни вартості активу V(t) часовий інтервал береться дуже коротким (нескінченно малим) dt, протягом якого інвестор може здійснювати вибір між вкладеннями в даний актив і доходом по депозиту. Нехай придбання даного активу (рішення приймається в момент (точці) часу t) дає інвесторові право на періодично отримуваний (купонний) дохід С(t), а також на отримання доходу від приросту нескінченно малої капітальної вартості активу в кінці розглядуваного періоду (dV). Інвестор здійснить вкладення коштів у придбання активу, якщо сумарна дохідність від інвестицій, тобто купонний дохід і приріст вартості активу, буде бодай не меншою, ніж дохід, гарантований даним станом ринку, наприклад від грошового депозиту того самого обсягу в надійному комерційному банку rV(t)dt. Оскільки майже завжди можна припускати виконання умови ненасичення, тобто раціональний інвестор завжди воліє мати якомога більший дохід (за допустимого ступеня ризику), то нерівність можна замінити на рівняння:
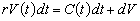 (16.2)
(16.2)
за відомої величини купонного доходу С(t) та ринкової ставки відсотка r. Рівняння (16.2), як заведено говорити, відображає умову відсутності арбітражного прибутку (no-arbitrage conditions), відіграє важливу роль у сучасній економічній і фінансовій теорії й уважається виконуваним на ефективних ринках.
У рівнянні (16.2) ліворуч стоїть величина, котра визначає вимоги інвестора щодо дохідності даного активу відповідно до ринкової ставки відсотка, праворуч — сума поточного доходу для облігації (чи дивіденду для акції) і приросту капітальної вартості активу за нескінченно малий період часу dt. Таким чином, інвестор обере даний актив (інвестує в нього) в тому разі, якщо його дохід буде не вищим і не нижчим за дохідність будь-якого іншого активу за ставкою ринкового відсотка r > 0. У протилежному випадку можливим є арбітраж, тобто отримання додаткового доходу за рахунок простого перерозподілу коштів, ресурсів. У випадку економічної рівноваги такі можливості відсутні, оскільки вибір є оптимальним, а тому сенс рівняння (16.2) полягає в описі умов економічної рівноваги, чи no-arbitrage conditions.
Відсутність умов арбітражу на ефективному ринку (16.2) можна проілюструвати з огляду на такі міркування. Припустимо протилежне: наприклад, дохід від даних вкладень (придбання даного активу) дещо вищий від ринкового, тобто має місце нерівність:
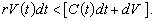
У цьому випадку раціонально діючий інвестор братиме позичку в банку за ринковою ставкою, якщо припустити існування такої можливості, та вкладатиме їх у даний актив, отже, зароблятиме на експлуатації ринкової недосконалості.
Однак, навіть якщо така можливість існує, то навряд чи вона існує досить тривалий час, оскільки в умовах вільної конкуренції збільшення заявок на позички примусить банки підвищити відсоток, а збільшення попиту на певний актив спричиниться до підвищення його ціни, знизивши тим самим його дохідність. Можна припустити, що ці процеси відбуватимуться доти, доки не встановиться рівняння (16.2). Навпаки, за нерівності

відсутність попиту на певний вид інвестицій приведе до зниження їхньої ціни, отже, і привабливості для інвесторів, тимчасом як численні депозити потягнуть за собою зниження банківського відсотка. Отже, розглянуті ситуації матимуть місце до встановлення тенденції ринкової рівноваги.
Таким чином, на ефективному ринку досконала конкуренція веде до вирівнювання «стандартної дохідності» й до ринкового відсотка. Відсутність умов арбітражу вважається надзвичайно важливою характеристикою ефективного ринку, котра означає, що безкоштовно ринок нічого не дає, а будь-яка можливість, що її надає ринок, обов’язково має свою ціну, котру треба сплачувати. Гіпотеза щодо ефективного ринку має важливе значення для сучасної теорії фінансів, а її адаптація для макроекономічних процесів значною мірою сприяє формуванню гіпотези раціональних очікувань і побудові моделі неокласичної рівноваги.
Created/Updated: 25.05.2018
 |
|