Главная Экономика Книги Моделювання економіки - Вітлінський В.В.

Моделювання економіки - Вітлінський В.В.

14.6. Фіскальний аспект динаміки боргу

Розгляньмо фіскальний аспект для детермінованого процесу дефіциту бюджету. Припустимо, що фінансування бюджетного дефіциту здійснюється лише за рахунок податків і нових боргів. Це означає, що бюджетний дефіцит і державний борг не викликають збільшення грошової маси, отже, не мають довготермінових інфляційних наслідків.

Якщо чинники монетарної природи, зокрема сеньйораж*2, відсутні, то накопичений упродовж певного періоду дефіцит бюджету являє собою обсяг державного боргу.

*2: {Сеньйораж — прибуток, одержаний державною скарбницею або центральним банком від випуску грошей. Дорівнює різниці між номінальною вартістю грошей та витратами на їхню емісію.}

Для обсягів державного боргу в реальних (поточних) цінах b = b(t) і неперервно нараховуваної додатної ставки дохідності за державними облігаціями r > 0 та гіпотези тривалих термінів накопичення дефіциту (практично нульового початкового боргу b(0) = 0) має місце співвідношення:

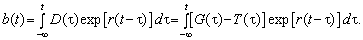(14.17)

Відповідно до (14.17) бюджет, котрий невизначено довго зводиться з дефіцитом D(t), характеризується наявністю у кожен момент часу t державного боргу обсягом b(t).

Виникає слушне запитання: наскільки великими можуть бути обсяги боргів, щоб у держави не виникало проблем щодо їх погашення? Відповідь на нього емпірично дається таким чином: оцінюються верхні межі для питомого боргу, який розуміють як відношення боргу (номінального) до ВВП (номінального). Вважається, що коли питомий борг не перевищує 50—70 %, то з його виплатами практично не буває проблем для зростаючої економіки. Теоретичне обґрунтування відповіді є дещо складнішим.

Позначимо питомий борг через :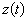

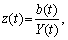
де Y(t) — обсяг реального ВВП у t-му році.

Зміна питомого боргу за нескінченно малий період часу 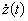дорівнюватиме:

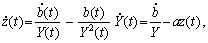(14.18)

де 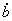— зміна реальних обсягів державного боргу за нескінченно малий період часу; — зміна реального ВВП за нескінченно малий період часу; — темпи приросту реального доходу (ВВП).

Приріст (нескінченно мале) реального боргу на момент часу t становить за визначенням величину бюджетного дефіциту:

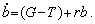(14.19)

Ця формула є просто іншим виразом рівняння державного боргу (14.17), якщо його продиференціювати за часом t (і навпаки).

Права частина рівняння (14.19) — це бюджетний дефіцит, котрий складається з первинного чи безвідсоткового дефіциту (G – T) і сплат по накопиченому боргу, що здійснюються за номінальною ставкою дохідності r державних облігацій. Підставляючи (14.19) у (14.18), отримаємо диференціальне рівняння стосовно до питомого боргу:

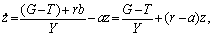
або

(14.20)

де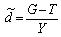 — величина (обсяг) питомого первинного дефіциту (дефіциту без урахування нарощених відсотків).

У рівнянні (14.20) структурний коефіцієнт і питомий первинний дефіцит 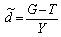можуть бути деякими функціями часу, що, взагалі кажучи, відповідає реальності, оскільки ставки відсотка, темпи зростання і частки дефіциту змінюються у часі. Однак для спрощення аналізу вважатимемо їх постійними величинами, значення котрих відомі:

Припустимо, що відоме і значення питомого боргу для деякого моменту часу, що береться за початковий, тобто z(0) = z0.

У даній моделі (за відсутності монетарних чинників) бюджетний дефіцит може фінансуватися в міру перевищення обсягів податків над поточними урядовими витратами, тобто за умови

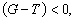
а також за рахунок нових позик.

Отже, помноживши обидві частини (14.20) на мінус одиницю і позначивши через 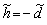величину бюджетного профіциту, одержимо рівняння фінансування бюджетного дефіциту (за відсутності сеньйоражу):

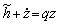, (14.21)

у котрому дефіцит зводиться лише до сплат накопиченого боргу за ставкою дохідності r > 0, скоригованою на величину a — темп приросту реального ВВП.

Для зростаючої економіки параметр a — додатне число, для економіки в стагнації — нуль, а для депресивної — від’ємне число.

Рівняння (14.21) показує, що бюджетний дефіцит (на одиницю продукту) qzзабезпечений у кожний момент часу чистими доходами держави і новими питомими боргами .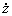

Заощадження витрат на обслуговування боргу за рахунок нових боргів є досить цікавим і породжує низку проблем.

Розгляньмо спочатку проблему фінансування бюджетного дефіциту без залучення нових позик, тобто за умови 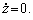Стан сталого (в часі) питомого боргу () є для системи (14.21) стаціонарним станом*3.

*3: {У деяких економічних працях пишуть про «стійкий стан», але це не точно, бо стаціонарний стан сам по собі може бути як стійким, так і нестійким, пов’язаним із ризиком.}

Для нього диференціальне рівняння (14.21) редукується до алгебраїчного рівняння, розв’язком котрого є функція:

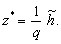(14.22)

Отже, якщо чисті доходи держави впродовж нескінченного періоду часу становлять величину 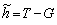, то ринкова вартість потоку цих доходів, приведена до теперішнього моменту часу, дорівнюватиме z*. Коефіцієнт капіталізації майбутніх потоків доходів — це величина 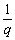, що має розмірність часу для q = (r – a) > 0.

Рівняння (14.21) є звичайним неоднорідним диференціальним рівнянням першого порядку, котре можна переписати у стандартному вигляді:

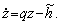(14.23)

Розв’язком (14.23) є функція питомого боргу, що відповідає обсягам його погашення:

(14.24)

Після знаходження розв’язку чи траєкторії (14.24) проблема обслуговування боргу, тобто здійснення регулярних сплат для його погашення, зводиться до дослідження поведінки траєкторії питомого боргу: якщо остання прямує до деякої постійної величини (стаціонарної точки чи стаціонарного стану), що не перевищує верхньої межі допустимого боргу, то борги можуть бути сплачені. У протилежному разі сплати асимптотично не є можливими, а банкрутство стає неминучим.

Нехай у деякий початковий момент часу t = 0 питомий борг, наприклад, перевищує цю початкову величину, тобто тоді проблема сплати боргів зводиться до того, щоб з’ясувати, зростає чи зменшується ця різниця у часі. Припустимо, що в період часу (0, t1) сплати по боргу не здійснюються, а починаються з моменту t1, коли вони стрибкоподібно дорівнюють 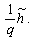Як випливає з розв’язку (14.24), питомий борг спочатку зростає експоненційно, а в момент t1 стрибкоподібно скорочується, оскільки починаються його сплати. Однак постійні сплати не впливають на динаміку питомого боргу, зростання якого триває, як це показано на рис. 14.2, лише за зміни початкових умов цього процесу. З аналізу розв’язку ясно, що такого характеру траєкторії боргу надає коефіцієнт q = (r – a) > 0, що являє собою різницю між ставкою реальної дохідності по державних облігаціях r і темпом приросту реального доходу a. Отже, якщо ставка дохідності державних облігацій r перевищує зростання доходу (ВВП чи національного доходу), то питомий борг зростає до нескінченності, оскільки економічних джерел покриття боргів не існує.

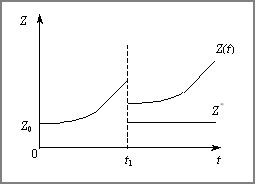
Рис. 14.2. Динаміка державного боргу

Нагадаймо, що сеньйораж у даній моделі відсутній, а економіка замкнута. Зрештою, замкнутість економіки тут не відіграє ніякої ролі, апелювання до зовнішніх джерел фінансування державного боргу для даної моделі не є суттєвим.

Формально траєкторія (14.24) вказує на те, що система сплати державного боргу є нестійкою. Навпаки, динаміка боргу стійка, тобто борги можуть бути сплачені лише тоді, коли реальний дохід зростає швидше, ніж величина ставки дохідності державних цінних паперів, тобто коли q < 0.

Економічний зміст даного висновку, на наш погляд, є надзвичайно важливим: за депресивної економіки борги не можуть бути сплачені, оскільки за a ? 0 система завжди є нестійкою.

Цікавим є й питання трансформаційних процесів у економіці, коли a = a(t) залежить від часу і є спадною функцією:

або або тощо.