Главная Экономика Книги Моделювання економіки - Вітлінський В.В.

Моделювання економіки - Вітлінський В.В.

11.2. Економіко-математична модель міжгалузевого балансу

Основу інформаційного забезпечення моделі міжгалузевого балансу становить технологічна матриця, що містить коефіцієнти прямих матеріальних витрат на виробництво одиниці продукції. Ця матриця є базою економіко-математичної моделі міжгалузевого балансу.

Припускається гіпотеза, згідно з якою для виробництва одиниці продукції в j-й галузі необхідна певна кількість витрат проміжної продукції і-ї галузі, що становить aij, і ця величина не залежить від обсягів виробництва в j-й галузі та є досить стабільною величиною в часі. Величини aij називають коефіцієнтами прямих матеріальних витрат та обчислюють таким чином:

(11.4)

Коефіцієнти прямих матеріальних витрат показують, яку кількість продукції і-ї галузі необхідно витратити, якщо враховувати лише прямі витрати, для виробництва одиниці продукції j-ї галузі. З урахуванням формули (11.4) систему рівнянь балансу (11.2) можна записати у вигляді

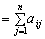Хі Хі (11.5)

Якщо ввести до розгляду матрицю коефіцієнтів прямих матеріальних витрат А = (аij), вектор-стовпчик валової продукції X та вектор-стовпчик кінцевої продукції Y:

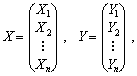
то система рівнянь (11.5) у матричній формі матиме вигляд

X = AX + Y . (11.6)

Систему рівнянь (11.5), чи у матричній формі (11.6), називають економіко-математичною моделлю міжгалузевого балансу (моделлю Леонтьєва, моделлю «витрати — випуск»). За допомогою цієї моделі можна виконати три варіанти обчислень:

• задаючи в моделі обсяги валової продукції кожної галузі (Хi), можна визначити обсяги кінцевої продукції кожної галузі(Yi):

Y = (E – A)X, (11.7)

де Е — одинична матриця n-го порядку;

• задаючи обсяги кінцевої продукції всіх галузей (Yi), можна визначити обсяги валової продукції кожної галузі (Хi):

X = (E – A)–1Y; (11.8)

• для низки галузей задаючи обсяги валової продукції, а для решти — обсяги кінцевої продукції, можна відшукати величини кінцевої та валової продукції всіх галузей.

У формулах (11.7) та (11.8) Е позначає одиничну матрицю n-го порядку, а (Е – А)–1 — матрицю, обернену до матриці (Е – А).

Якщо визначник матриці (Е – А) не дорівнює нулеві, тобто ця матриця не вироджена, тоді існує матриця, обернена до неї. Позначимо цю матрицю через В:

B = (Е – А)–1. (11.9)

Систему рівнянь у матричній формі (11.8) можна записати:

X = BY . (11.10)

Елементи матриці В позначатимемо через bij , тоді з матричного рівняння (11.10) для будь-якої і-ї галузі можна отримати співвідношення:

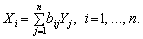(11.11)

Із співвідношення (11.11) випливає, що валова продукція постає як зважена сума обсягів кінцевої продукції, ваговими коефіцієнтами тут є bіj, котрі показують, скільки всього необхідно виробити валової продукції і-ї галузі для випуску у сферу кінцевого використання одиниці продукції j-ї галузі. На відміну від коефіцієнтів прямих витрат aij , коефіцієнти bіj називають коефіцієнтами повних матеріальних витрат, і вони включають у себе як прямі, так і опосередковані витрати всіх порядків. Якщо прямі витрати відбивають кількість засобів виробництва, використаних безпосередньо на виготовлення певних обсягів даного продукту, то опосередковані стосуються попередніх стадій виробництва і входять у виробництво продукції не прямо, а через інші (проміжні) засоби виробництва.

Коефіцієнти повних матеріальних витрат bij показують, який обсяг продукції j-ї галузі необхідно виробити, щоб з урахуванням прямих і опосередкованих витрат цієї продукції отримати одиницю кінцевої продукції j-ї галузі.

Коефіцієнти повних матеріальних витрат можна застосовувати, коли необхідно визначити, як вплинуть на валовий випуск певної галузі деякі зміни щодо обсягів випуску кінцевої продукції всіх галузей:

(11.12)

де DXi та DYj — зміни (прирости) обсягів валової й кінцевої продукції відповідно.