- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Экономика Экономика  Книги Книги  Моделювання економіки - Вітлінський В.В. Моделювання економіки - Вітлінський В.В. |
Моделювання економіки - Вітлінський В.В.
4.2. Взаємозалік боргів підприємств
Будь-яка досить значна за своїми масштабами економічна система містить у собі десятки тисяч підприємств (фірм, корпорацій тощо), які обмінюються між собою товарами та послугами. Навіть дрібна фірма, що має відносно невелику кількість партнерів, опосередковано поєднана (через зв’язки прямих та опосередкованих партнерів) з величезною кількістю підприємств, що утворюють систему, і її процвітання безпосередньо залежить від їхнього стану.
Взаємозалежність усіх ланок економічної системи добре проявляється через проведення розрахунків між підприємствами за поставлену продукцію. Отримавши від своїх клієнтів виручку за товар, підприємство витрачає її на закупівлю сировини та обладнання в інших фірм, на заробітну плату (тобто на купівлю робочої сили), на рекламу тощо, що є необхідним для його нормального функціонування. Отже, в економічний обіг залучається велика кількість партнерів даного підприємства.
Насправді ж між постачанням товару та оплатою за нього завжди існує затримка в часі. Її мінімальне значення визначається суто технічними причинами, бо потрібен певний час на транспортування та розфасування товару, здійснення банківських операцій тощо.
Однак можливі ситуації, коли з якихось економічних, фінансових, соціальних, психологічних, політичних та інших причин час затримки сплати (постачання) стає порівнянним з часом обігу фінансів, а абсолютне значення (обсяг) невиконаних сплат чи поставок — порівнянним з обсягом вільних обігових коштів підприємства. У цьому разі виникає так звана криза несплат, котра може спричинити кризу всієї економічної системи.
Підприємство, що не отримало гроші за поставлену продукцію (чи заплатило за товар, але не отримало його), не в змозі розрахуватися зі своїми постачальниками (оскільки обсяг його боргів рівний чи перевищує обсяги його вільних коштів). У свою чергу постачальники не розраховуються зі своїми клієнтами, ті — зі своїми і так далі. Виникають довгі ланцюжки несплат, що пронизують усю систему. Вони, очевидно, можуть складатися з N ланок, а загальна кількість їх досягає числа близько N! (N — кількість підприємств).
Пояснимо сутність проблеми на простому числовому прикладі для системи, що складається з трьох підприємств, кожне з яких має вільні кошти, що дорівнюють одній фінансовій умовній одиниці, а основні фонди дорівнюють 10 одиницям. Нехай перше підприємство винне другому 100 одиниць, друге винне третьому 100 одиниць, а третє — першому також 100 одиниць. Сумарний абсолютний борг підприємств дорівнює 300 одиницям і порівняно з їхніми фондами (30 одиниць) є величезним. У той же час фінансовий стан цієї системи є непоганим, оскільки сумарний «борг» кожного підприємства, окремо взятого, дорівнює нулеві. Очевидно, процедура взаємозаліку полягає в одномоментному анулюванні (погашенні) усіх боргів: оголошується, що ніхто нікому не винен, і партнери продовжують функціонувати, будучи вільними від боргового тягаря.
Подібну операцію, виконану «вручну», неможливо, звичайно ж, реалізувати для великої кількості підприємств. Необхідні більш глибокі підходи, для розгляду котрих треба формалізувати задачу.
Нехай економічна система складається з N підприємств, які можуть мати взаємні борги. Позначимо борги n-го підприємства m-му підприємству через xnm, де 1 ? n, m ? N (xnп < 0, якщо перше підприємство (n) винне другому (m), i xnm > 0 — у протилежному випадку). Ясно, що
xnm =– xnm, xnп = 0,
тобто сукупність боргів описується кососиметричною матрицею розмірності N ? N з нульовою діагоналлю (xnп = 0, бо підприємство не може бути винне само собі). Сума всіх взаємних боргів обчислюється за формулою:
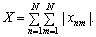 (4.7)
(4.7)
Величина Х (4.7) є однією з інтегральних кількісних характеристик фінансового стану системи, якщо вона має порядок, однаковий із сумою всіх вільних коштів підприємства (Х0), тобто:
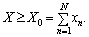 (4.8)
(4.8)
Ситуація, що описується нерівністю (4.8), власне, означає кризу несплат (тут xn ? 0 — індивідуальні власні засоби підприємств).
Ще однією важливою характеристикою є баланс кредитів і боргів (сальдо) кожного підприємства:
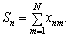 (4.9)
(4.9)
Зазначимо, що, як видно з (4.9), можливими є варіанти Sn > 0; Sn < 0; Sn = 0. Якщо Sn > 0, то підприємство в певному розумінні є кредитором підприємств-боржників, тобто тих, у кого Sn < 0 (якщо Sn = 0, то таке підприємство вважається «нейтральним» щодо боргів). Якщо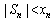 , то індивідуальний фінансовий стан підприємства є, по суті, нормальним, оскільки його реальні сумарні борги (чи кредити) менші, ніж його вільні засоби (кошти). Аналогічно сумарне абсолютне сальдо системи
, то індивідуальний фінансовий стан підприємства є, по суті, нормальним, оскільки його реальні сумарні борги (чи кредити) менші, ніж його вільні засоби (кошти). Аналогічно сумарне абсолютне сальдо системи
 (4.10)
(4.10)
є макропоказником її можливого фінансового «здоров’я». Якщо S < X0, то вільних коштів у системі більше, ніж дійсних боргів, і потенційно вона може успішно функціонувати. Між величинами X та S завжди існує певне співвідношення. Для будь-якої довільної матриці боргів виконується нерівність:
X ? S, (4.11)
тобто сумарний борг не може бути меншим за сумарне сальдо.
Завдання щодо погашення взаємних боргів полягає в тому, щоб, знаючи матрицю Х, відшукати матрицю «нових» боргів Х', для котрої б виконувалася умова X' < X. Очевидно, що ідеальним її розв’язком був би такий, щоб X' = S, тобто щоб нерівність (4.10) стала рівнянням. Зазначимо, що тоді для такої, що є безпечною по суті, системи з S ? X0 виконувалось би співвідношення X' = S ? X0, і після взаємозаліку вона могла б нормально функціонувати (хоча зменшення обсягів Х у будь-якому випадку є сприятливим).
Будуючи математичну модель процедури взаємозаліків, використовуватимемо низку операцій. Перша — це відмова, на певному етапі, від детального розгляду множини індивідуальних боргів і відповідних зв’язків між підприємствами. Перехід з мікрорівня на макрорівень.
Зазначимо, що процедура моніторингу ланцюжків для N підприємств має принциповий недолік. Розгляньмо спочатку ланцюжок, у якому кожне підприємство з першого до М-го (M ? N) винне іншому однакову суму, і таку ж суму винне М-те підприємство першому (рис. 4.1).
Ланцюжок є замкненим, і розв’язок є очевидним — усі борги в ланцюжку погашаються. Нехай тепер М-те підприємство не винне нічого 1-му (рис. 4.2).
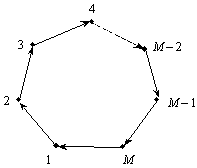
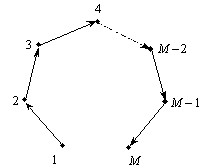
Рис. 4.1 Рис. 4.
Ланцюжок розімкнений, і цей метод є непридатним. У той же час просте рішення полягає в тім, що борги підприємств з другого до (М – 1)-го не анулюються, а борг першого переадресовується М-му (рис. 4.3).
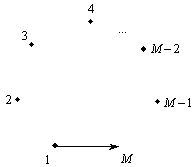
Рис. 4.3
Економічний сенс переадресації відповідає суті вексельного обігу, коли боргове зобов’язання змінює своїх хазяїв, і в результаті у боржника (перше підприємство) з’являється новий кредитор (М-не підприємство).
На відміну від ситуації з боргами в ланцюжках повна система боргів по всіх ланцюжках є замкненою, бо розглядаються взаємні борги. Справді, з властивості xnm = – xmn маємо, що
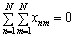
для будь-якої сукупності несплат. Враховуючи, що 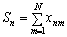 , з останнього рівняння дістаємо
, з останнього рівняння дістаємо
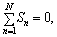 (4.12)
(4.12)
або сума додатних сальдо підприємств дорівнює за абсолютною величиною сумі від’ємних сальдо, тобто
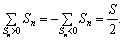 (4.13)
(4.13)
Отже, якщо розглядати на макроекономічному рівні систему взаємних боргів, то вона має властивість «симетричної консервативності».
Рівняння (4.13) пояснює структуру для побудови математичної моделі ідеального взаємозаліку, який відбувається за таких умов:
1) усі борги xnm відомі й визнаються підприємствами;
2) після проведення взаємозаліку сальдо підприємств Sn залишаються незмінними:  , тобто індивідуальний фінансовий стан кожного з них не змінюється;
, тобто індивідуальний фінансовий стан кожного з них не змінюється;
3) частина боргів xnm списується, а частина переадресовується, тобто у підприємств можуть як з’явитися нові боржники та кредитори, так і частково зникнути старі.
Зміст макропроцедури взаємозаліку полягає в тому, що замість величин xnm розглядаються величини Sn. Підприємства з Sn < 0 оголошуються боржниками (в обсязі свого сальдо), а підприємства з Sn > 0 — кредиторами (в тих самих обсягах). Після цього борги підприємств з Sn < 0 певним чином розподіляються між кредиторами, тобто будується нова система боргів xnm. У цьому разі виконується друга умова і досягається рівність X' = S, тому розв’язок задачі якоюсь мірою є раціональним. Таких розв’язків, взагалі кажучи, може бути багато, бо розподіляти борги між кредиторами можна різними способами. Наведемо два найпростіших.
Перший можна подати за допомогою формули, згідно з якою нові борги обчислюються через старі:
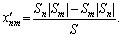 (4.14)
(4.14)
Згідно з (4.14) борг будь-якого підприємства (обсяг якого Sn, якщо Sn < 0) між підприємствами-кредиторами розподіляється у частках, пропорційних обсягам їхнього сальдо (що дорівнюють Sm, якщо Sm > 0). Підприємству, що має більше за обсягом позитивне сальдо, нараховується від кожного з боржників більша частка його боргів, у сумі вони дають величину Sm. Для підприємств із нульовим сальдо взаємозалік зводиться до погашення всіх їхніх боргів і всіх боргів їм. Зазначимо, що в (4.14) для нових боргів маємо 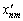 , коли Sn < 0, Sm < 0 чи коли Sn > 0, Sm > 0 (після взаємозаліку боржники не винні боржникам, а кредитори — кредиторам). Це означає, що кількість отриманих фінансових зв’язків між підприємствами значно менша за максимально можливу, коли кожне підприємство є одночасно і боржником, і кредитором будь-якого іншого, а матриця боргів не має нульових елементів (окрім, звичайно, діагональних).
, коли Sn < 0, Sm < 0 чи коли Sn > 0, Sm > 0 (після взаємозаліку боржники не винні боржникам, а кредитори — кредиторам). Це означає, що кількість отриманих фінансових зв’язків між підприємствами значно менша за максимально можливу, коли кожне підприємство є одночасно і боржником, і кредитором будь-якого іншого, а матриця боргів не має нульових елементів (окрім, звичайно, діагональних).
Другий спосіб ґрунтується на тому, що кількість зв’язків може бути значно зменшена, якщо провести попереднє впорядкування підприємств згідно з абсолютними значеннями їхніх сальдо та встановити безпосередні зв’язки між боржниками й кредиторами одного масштабу (великі з великими, малі з малими). Ця процедура допускає просту геометричну інтерпретацію. На рис. 4.4 на верхній прямій лінії описано розподіл сальдо кредиторів (у спадній послідовності). Довжина відрізків цієї прямої дорівнює обсягові сальдо кожного підприємства Sp > 0, 1 < p < N, а її загальна довжина, очевидно — S/2.

Рис. 4.4
На нижній прямій описано розподіл сальдо боржників Sq < 0, 1 < q < N, p + q ? N (сальдо взяті з оберненим знаком) також у спадній послідовності. Її довжина згідно з (4.13) також дорівнює S/2. Штрихові лінії, що проведені з вузлів нижньої прямої, поділяють «пряму кредиторів» на q відрізків, що дорівнюють обсягам боргу кожного підприємства. Цей борг або дістається одному кредиторові, або ділиться між кількома відповідно до розташування вузлів верхньої прямої відносно даного відрізка.
Описаний алгоритм є раціональним за критерієм X' = S і, очевидно, оптимальним за кількістю зв’язків, що залишилися після взаємозаліку.
Приклад взаємозаліку в системі з N = 10 і початковою матрицею боргів з 90 ненульовими недіагональними елементами наведено в таблиці 4.1. Кінцева матриця містить лише 14 ненульових елементів. У спеціальних випадках в одного боржника залишається один кредитор, і навпаки.
Таблиця 4.1
Приклад взаємозаліку в системі з N = 10 і початковою матрицею боргів з 90 ненульовими недіагональними елементами
| № з/п | 1 | 2 | 3 | 4 | 6 | 6 | 7 | 8 | 9 |
Початкова матриця (Х = 3729) | |||||||||
2 | 25 |
|
|
|
|
|
|
|
|
3 | –1 | –20 |
|
|
|
|
|
|
|
4 | 4 | 25 | –2 |
|
|
|
|
|
|
5 | 25 | –450 | 25 | 30 |
|
|
|
|
|
6 | –15 | 150 | –30 | 20 | –928 |
|
|
|
|
7 | 3 | –40 | 3 | 3 | 5 | 25 |
|
|
|
8 | 1 | –22 | –2 | –2 | 4 | –15 | 5 |
|
|
9 | 10 | 322 | –15 | –25 | 498 | –800 | –10 | 20 |
|
10 | 1 | –25 | –2 | 1 | –20 | 15 | –1 | –3 | 30 |
Кінцева матриця (X' = S = 62) | |||||||||
2 | 2 |
|
|
|
|
|
|
|
|
3 | 0 | 0 |
|
|
|
|
|
|
|
4 | 0 | 0 | 0 |
|
|
|
|
|
|
5 | 0 | 0 | 0 | 0 |
|
|
|
|
|
6 | 0 | 0 | 0 | 0 | –28 |
|
|
|
|
7 | 1 | 0 | 0 | 0 | 0 | 0 |
|
|
|
8 | 0 | –7 | 0 | 0 | 0 | 0 | 0 |
|
|
9 | 0 | –18 | 0 | 0 | –2 | 0 | 0 | 0 |
|
10 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 |
Зазначимо, що наведені та інші процедури взаємозаліку мають сенс лише за виконання умов 1—3, тобто коли є відповідна угода між підприємствами. Причини, що не дозволяють дотримуватися даної угоди, можуть бути досить різноманітними — від небажання сплачувати борги, тому що це вигідно боржникові, до наслідків санкцій міжнародних чи інших організацій, коли фінансові кошти підприємств «заморожуються».
Created/Updated: 25.05.2018
 |
|