Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

9.4. Принцип оптимальності

З викладених у попередніх параграфах міркувань можна висновувати, що для прийняття оптимального рішення на k-му кроці багатокрокового процесу потрібна оптимальність рішень на всіх його попередніх кроках, а сукупність усіх рішень дає оптимальний розв’язок задачі лише в тому разі, коли на кожному кроці приймається оптимальне рішення, що залежить від параметра етапу 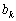, визначеного на попередньому кроці.

Цей факт є основою методу динамічного програмування і є сутністю так званого принципу оптимальності Р. Белмана, який формулюється так:

Оптимальний розв’язок багатокрокової задачі має ту властивість, що яким би не був стан системи 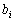в результаті деякої кількості кроків, необхідно вибирати управління на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний.

Доведемо справедливість такого твердження, міркуючи від супротивного. Нехай маємо задачу на максимізацію функції 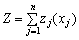і вектор 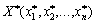є її оптимальним планом (стратегією, поведінкою) n-крокового процесу (n-вимірної задачі) з початковим параметром стану b.

Принцип оптимальності еквівалентний твердженню, що вектор повинен бути оптимальним планом 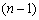-крокового процесу 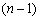-вимірної задачі з початковим параметром стану 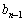, що дорівнює 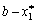. Припустимо протилежне, тобто що вектор 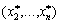не є оптимальним планом відповідного процесу, а ним є якийсь інший план 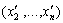. Тоді дістанемо:

,

але

,

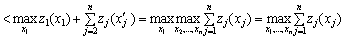що суперечливо. Отже, принцип оптимальності доведено.