- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
8.5. Необхідні умови існування сідлової точки
Для розроблення методів розв’язування окремих типів задач нелінійного програмування важливе значення має поняття сідлової точки, а також визначення необхідних і достатніх умов існування сідлових точок функції Лагранжа 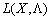 у (n + m)-вимірному просторі змінних
у (n + m)-вимірному просторі змінних 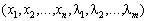 за довільних умов, які можуть накладатися на їх знаки (необхідні і достатні умови існування сідлової точки функції Лагранжа за відсутності обмежень на знаки змінних розглянуто в § 8.4).
за довільних умов, які можуть накладатися на їх знаки (необхідні і достатні умови існування сідлової точки функції Лагранжа за відсутності обмежень на знаки змінних розглянуто в § 8.4).
Розглянемо нелінійну задачу:
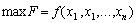 ,
,
 .
.
Причому на компоненти векторів 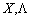 накладено обмеження на знаки. Позначимо множину точок, що задовольняють такі обмеження, через
накладено обмеження на знаки. Позначимо множину точок, що задовольняють такі обмеження, через  .
.
Функція Лагранжа для цієї задачі має вигляд:
 =
=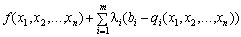 . (8.12)
. (8.12)
Точка  називається сідловою точкою функції Лагранжа (8.12), якщо для всіх
називається сідловою точкою функції Лагранжа (8.12), якщо для всіх  виконується співвідношення:
виконується співвідношення:
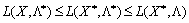 . (8.13)
. (8.13)
Для диференційовних функцій 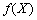 та
та 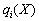 знайдемо необхідні умови існування сідлової точки.
знайдемо необхідні умови існування сідлової точки.
Сідлова точка 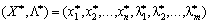 функції
функції 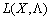 виду (8.12) за означенням задовольняє умову:
виду (8.12) за означенням задовольняє умову:
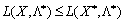 .
.
Нерівність виконується для всіх точок Х, тобто також і для тих, у яких лише одна координата відрізняється від Х*. Допустимо, що це хk, а всі інші збігаються з координатами сідлової точки 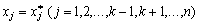 .
.
 Оскільки права частина нерівності є фіксованою, а в лівій частині змінюється лише одна координата хk, то приходимо до функції однієї змінної
Оскільки права частина нерівності є фіксованою, а в лівій частині змінюється лише одна координата хk, то приходимо до функції однієї змінної 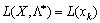 , яку можна зобразити графічно на координатній площині.
, яку можна зобразити графічно на координатній площині.
Розглянемо спочатку випадок, коли 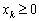 , тобто лише частину координатної площини, для якої
, тобто лише частину координатної площини, для якої 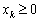 .
.
Можливі такі випадки:
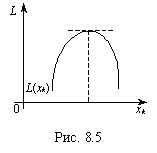
1) коли всі  , то максимальне значення функції L(xk) досягатиметься в точці, для якої
, то максимальне значення функції L(xk) досягатиметься в точці, для якої 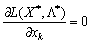 (рис. 8.5).
(рис. 8.5).
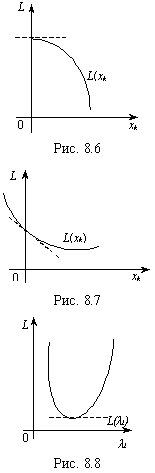 2) коли максимум функції L(xk) досягатиметься в точці
2) коли максимум функції L(xk) досягатиметься в точці 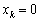 і розглядувана частинна похідна також дорівнюватиме нулю:
і розглядувана частинна похідна також дорівнюватиме нулю: 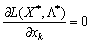 (рис. 8.6).
(рис. 8.6).
3) коли точка максимуму функції L(xk) досягатиметься також у точці 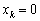 , а частинна похідна
, а частинна похідна 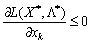 (рис. 8.7).
(рис. 8.7).
Узагальнюючи всі три ситуації, маємо:
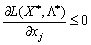 для
для 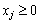
та 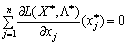 .
.
Розглядаючи другу частину нерівності (8.13):
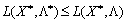
аналогічними міркуваннями, що проілюстровані рис. 8.8.—8.10, встановлюються необхідні умови для похідних по 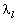 функції Лагранжа в сідловій точці.
функції Лагранжа в сідловій точці.

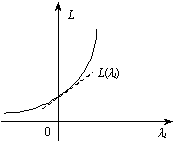
Рис. 8.9 Рис. 8.10
Об’єднуючи всі три випадки для невід’ємних координат, маємо необхідні умови сідлової точки:
 для тих індексів j, де
для тих індексів j, де 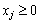 . (8.14)
. (8.14)
Зауважимо, що для  маємо ті самі випадки, які зображено на рис. 8.1—8.6, причому графіки будуть симетрично відображені відносно осі Оy, тобто для недодатних координат необхідна умова має вигляд:
маємо ті самі випадки, які зображено на рис. 8.1—8.6, причому графіки будуть симетрично відображені відносно осі Оy, тобто для недодатних координат необхідна умова має вигляд:
 для тих індексів j, де
для тих індексів j, де 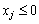 . (8.15)
. (8.15)
І нарешті, як відомо з попереднього параграфа, якщо на знак хj умови не накладаються, то необхідною умовою є:
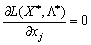 ,
, 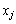 — довільного знака. (8.16)
— довільного знака. (8.16)
Узагальнення всіх випадків приводить до рівняння:
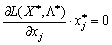 . (8.17)
. (8.17)
Розглядаючи другу частину нерівності (8.13), за допомогою аналогічних міркувань встановлюємо необхідні умови для похідних по 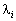 функції Лагранжа в сідловій точці:
функції Лагранжа в сідловій точці:
 для тих індексів і, де
для тих індексів і, де 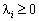 , (8.18)
, (8.18)
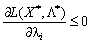 для тих індексів і, де
для тих індексів і, де 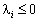 , (8.19)
, (8.19)
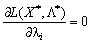 для тих індексів і, де
для тих індексів і, де 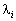 має довільний знак. (8.20)
має довільний знак. (8.20)
Отже, справджується рівняння:
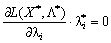 . (8.21)
. (8.21)
Сукупність співвідношень (8.14)—(8.21) становить необхідні умови, які має задовольняти сідлова точка 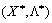 функції Лагранжа для точок, що належать множині
функції Лагранжа для точок, що належать множині 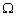 . При цьому
. При цьому  повинна мати частинні похідні по всіх компонентах векторів
повинна мати частинні похідні по всіх компонентах векторів 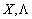 .
.
Created/Updated: 25.05.2018
 |
|