Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

РОЗДІЛ 5. ТРАНСПОРТНА ЗАДАЧА

«Во всех частях земного шара

имеются свои, даже иногда очень

любопытные другие части»

Сочинения Козьмы Пруткова

Транспортна задача є типовою задачею лінійного програмування, отже, її розв’язок можна отримати звичайним симплексним методом. Однак, у деяких випадках застосування універсальних алгоритмів є нераціональним. Специфічна структура транспортної задачі дає змогу отримати альтернативний метод відшукання оптимального плану у вигляді простішої у порівнянні з симплексним методом обчислювальної процедури. Транспортна задача належить до типу розподільчих задач лінійного програмування. Економічний зміст таких задач може стосуватися різноманітних проблем, що переважно зовсім не пов’язано із перевезенням вантажів, як, наприклад, задачі оптимального розміщення виробництва, складів, оптимального призначення тощо. Деякі з таких задач розглянемо в цьому розділі.

5.1. Економічна і математична постановка транспортної задачі

Класична транспортна задача лінійного програмування формулюється так: деякий однорідний продукт, що знаходиться у m постачальників Аі в обсягах 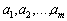одиниць відповідно необхідно перевезти n споживачам 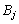в обсягах 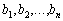одиниць. При цьому виконується умова, що загальний наявний обсяг продукції у постачальників дорівнює загальному попиту всіх споживачів. Відомі вартості 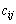перевезень одиниці продукції від кожного Аі-го постачальника до кожного Вj-го споживача, що подані як елементи матриці виду:

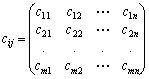
Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімальною.

У такій постановці задачі ефективність плану перевезень визначається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень.

Запишемо її математичну модель. Позначимо через 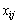обсяг продукції, що перевозиться від 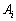постачальника до 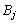споживача 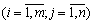. Тоді умови задачі зручно подати у вигляді такої таблиці:

Таблиця 5.1

Мають виконуватися такі умови:

1. сумарний обсяг продукції, що вивозиться з кожного і-го пункту, має дорівнювати запасу продукції в даному пункті:

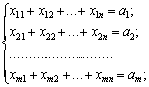
1. сумарний обсяг продукції, що ввезений кожному j-му споживачеві, має дорівнювати його потребам:

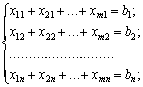
1. сумарна вартість всіх перевезень повинна бути мінімальною:

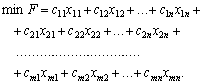
Очевидно, що .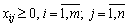

У скороченій формі запису математична модель транспортної задачі за критерієм вартості перевезень має такий вигляд:

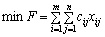(5.1)

за обмежень:

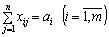; (5.2)

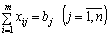; (5.3)

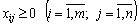. (5.4)

У розглянутій задачі має виконуватися умова:

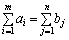. (5.5)

Транспортну задачу називають збалансованою, або закритою, якщо виконується умова (5.5). Якщо ж така умова не виконується, то транспортну задачу називають незбалансованою, або відкритою.

Домовимося планом транспортної задачі називати будь-який невід’ємний розв’язок системи обмежень (5.2)—(5.4), який позначають матрицею 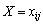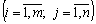. Значення невідомих величин — обсяги продукції, що мають бути перевезені від i-х постачальників до j-х споживачів, називатимемо перевезеннями.

Оптимальним планом транспортної задачі називають матрицю 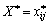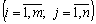, яка задовольняє умови задачі, і для якої цільова функція (5.1) набирає найменшого значення.

Теорема (умова існування розв’язку транспортної задачі): необхідною і достатньою умовою існування розв’язку транспортної задачі (5.1)—(5.4) є її збалансованість: .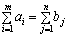

Доведення. Необхідність. Нехай задача (5.1)—(5.4) має розв’язок 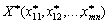, тоді для нього виконуються рівняння-обмеження (5.2) і (5.3). Підсумуємо відповідно ліві та праві частини систем рівнянь (5.2) і (5.3). Матимемо:

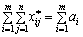, (5.6)

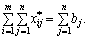(5.7)

Оскільки ліві частини рівнянь (5.6) та (5.7) збігаються, то праві також рівні одна одній, отже, виконується умова:

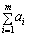
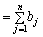. (5.8)

Достатність. Потрібно показати, що за заданої умови (5.8) існує хоча б один план задачі, і цільова функція на множині планів обмежена.

Нехай 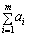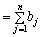= W > 0. Розглянемо величини 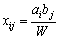(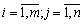). Підставивши значення 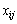в систему обмежень задачі (5.1)—(5.4), матимемо:

;

.

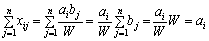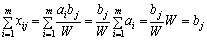Оскільки умови (5.2) та (5.3) виконуються, то 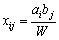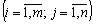є планом наведеної транспортної задачі.

Виберемо з елементів 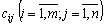найбільше значення і позначимо його через . Якщо замінити в цільовій функції (5.1) всі коефіцієнти на 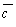, то, враховуючи (5.2), матимемо:

.

Виберемо з елементів найменше значення і позначимо його через 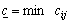. Якщо замінити в цільовій функції (5.1) всі коефіцієнти на 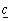, то, враховуючи (5.2), матимемо:

.

Тобто цільова функція на множині допустимих планів транспортної задачі є обмеженою:

.

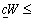
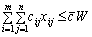Теорему доведено.

Якщо при перевірці збалансованості (5.5) виявилося, що транспортна задача є відкритою, то її необхідно звести до закритого типу. Це здійснюється введенням фіктивного (умовного) постачальника 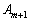у разі перевищення загального попиту над запасами 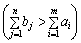із ресурсом обсягом . Якщо ж загальні запаси постачальників перевищують попит споживачів 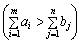, то до закритого типу задача зводиться введенням фіктивного (умовного) споживача 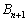з потребою .

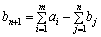Вартість перевезення одиниці продукції від фіктивного постачальника (або фіктивного споживача 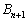) до кожного зі споживачів (виробників) має дорівнювати нулю або бути набагато більшою за реальні витрати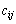 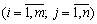. Як правило, у такому разі використовують нульові значення вартостей перевезень, що дає змогу спростити обчислення.

Як згадувалося вище, транспортна задача (5.1)—(5.4) є звичайною задачею лінійного програмування і може бути розв’язана симплексним методом, однак особливості побудови математичної моделі транспортної задачі дають змогу розв’язати її простіше. Легко помітити, що всі коефіцієнти при змінних у рівняннях (5.2), (5.3) дорівнюють одиниці, а сама система обмежень (5.2), (5.3) задана в канонічній формі. Крім того, система обмежень (5.2), (5.3) складається з mn невідомих та m + n рівнянь, які пов’язані між собою співвідношенням (5.8). Якщо додати відповідно праві та ліві частини систем рівнянь (5.2) та (5.3), то отримаємо два однакових рівняння:

;

.

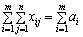
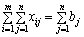
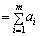Наявність у системі обмежень двох однакових рівнянь свідчить про її лінійну залежність. Якщо одне з цих рівнянь відкинути, то в загальному випадку система обмежень буде містити m + n – 1 лінійно незалежне рівняння, отже, їх можна розв’язати відносно m + n – 1 базисних змінних. Назвемо опорним планом транспортної задачі такий допустимий її план, що містить не більш ніж m + n – 1 додатних компонент, а всі інші його компоненти дорівнюють нулю. Такий план є невиродженим. Якщо ж кількість базисних змінних менша ніж m + n – 1, то маємо вироджений опорний план.