Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

4.3. Оцінка рентабельності продукції, яка виробляється, і нової продукції

Оцінку рентабельності продукції, що виготовляється на підприємстві, можна здійснювати за допомогою двоїстих оцінок та обмежень двоїстої задачі, які характеризують кожний вид продукції.

Ліва частина кожного обмеження двоїстої задачі є вартістю відповідних ресурсів, які використовують для виробництва одиниці j-ї продукції. Якщо ця величина перевищує ціну одиниці продукції (сj), то виготовляти таку продукцію невигідно, вона нерентабельна і в оптимальному плані прямої задачі відповідна їй змінна хj = 0. Якщо ж загальна оцінка всіх ресурсів дорівнює ціні одиниці продукції, то виготовляти таку продукцію доцільно, вона рентабельна і в оптимальному плані прямої задачі відповідна змінна хj > 0.

Підставимо значення оптимального плану двоїстої задачі Y* у її систему обмежень. Якщо вартість ресурсів на виробництво одиниці продукції (ліва частина обмеження) перевищує ціну цієї продукції (права частина обмеження), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.

Аналогічні результати можна дістати, проаналізувавши додаткові змінні оптимального плану двоїстої задачі (§ 4.2). Як з’ясовано вище, значення додаткових змінних показують, наскільки вартість ресурсів перевищує ціну одиниці відповідної продукції. Тому, якщо додаткова змінна двоїстої задачі дорівнює нулю, то продукція рентабельна. І, навпаки, якщо уі > 0, то відповідна продукція нерентабельна.

Оптимальні значення у4 = 5 > 0; у5 = 5/2 > 0, тому продукція А і В нерентабельна, а у6 = 0; у7 = 0, тобто продукція С і D — рентабельна.

Дослідимо питання про доцільність введення нового (n + 1)-го виду продукції, якщо відомі витрати кожного ресурсу на виготовлення одиниці такої продукції — 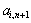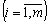і ціна її реалізації — . За умови введення у виробництво нового виду продукції в економіко-математичну модель (4.7) необхідно ввести відповідну змінну (хn+1). Отже, модель прямої задачі набуде вигляду:

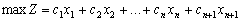
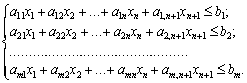
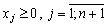
Відповідна математична модель двоїстої задачі міститиме не n, а (n + 1) нерівність і відрізнятиметься від (4.8) наявністю обмеження, що описує витрати на виробництво нового виду продукції:

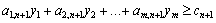(4.9)

Оскільки значення 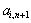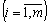і за умовою задачі відомі, розраховані також значення , то можна перевірити виконання нерівності (4.9). Як зазначено вище, рентабельною є продукція, для якої відповідне обмеження виконується як рівняння, а нерентабельною, якщо ліва частина нерівності (витрати ресурсів на виробництво одиниці продукції) перевищує праву (ціну реалізації одиниці продукції).

Допустимо, що за умов прикладу 4.1 запропоновано включити у виробництво один з двох видів нової продукції: E чи G. Відомі витрати кожного ресурсу на виготовлення одиниці цих видів продукції, що становлять для продукції виду E відповідно 4, 7, 2 ум. од. та для продукції виду G — 4, 8, 1 ум. од. Ціна реалізації одиниці продукції обох нових видів однакова і дорівнює 4,5 ум. од.

Складемо відповідне обмеження двоїстої задачі. Наступний вид продукції буде позначатися через х5, тому маємо:

.

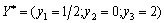Перевіримо виконання обмеження спочатку для продукції виду Е:

;

.

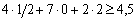Обмеження виконується як строга нерівність, отже, за умов даного підприємства виробництво продукції Е є недоцільним.

Зауважимо, що остання нерівність визначає мінімальне значення ціни реалізації одиниці продукції, за якої її випуск є рентабельним. Отже, ціна одиниці продукції Е за даних умов має становити не менше 6 ум. од.

Визначимо співвідношення між витратами на виробництво та ціною для продукції G:

.

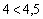З останньої нерівності маємо, що витрати на виробництво одиниці продукції G менші, ніж ціна реалізації. Така продукція є рентабельною за умов виробництва, на даному підприємстві і її доцільно включити в план випуску.

Для визначення оптимального плану виробництва із введеним додатково видом продукції обов’язково необхідно розв’язати нову задачу лінійного програмування. Двоїсті оцінки лише показують, доцільне чи ні розв’язання такої задачі.