- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
Заключні зауваження
Поняття двоїстості задач лінійного програмування має велике значення не лише в теоретичному плані, але й широко застосовується для обґрунтування та прийняття практичних рішень. Двоїстість у лінійному програмуванні була розроблена академіком Л. В. Канторовичем ще 1933 року. 1975 року Л. В. Канторович і американський математик Г. Купманс за відкриття теорії двоїстості та її застосування в економічних дослідженнях одержали Нобелівську премію. Значні теоретичні досягнення в цій галузі мали В. В. Новожилов, В. С. Нємчинов, А. І. Лур’є, В. С. Михалевич, Ю. М. Єрмолєв та інші вчені.
Двоїсті задачі мають чітку геометричну та економічну інтерпретацію. Теореми двоїстості широко використовуються в економічних дослідженнях. У 70-х роках у Радянському Союзі велась дискусія з приводу застосування двоїстих оцінок в економіці. Економісти того часу недооцінювали цю важливу економічну категорію. Проблема полягала ще й у тому, що ціни в Радянському Союзі були необґрунтованими. При визначенні рівня цін, що здебільшого встановлювалось адміністративно, не враховувались реальні витрати живої та уречевленої праці, попит на продукцію та її пропозиція на ринку. Радянські економісти також не розуміли, чому недефіцитні ресурси мають нульову оцінку.
Контрольні запитання
- У чому сутність теорії двоїстості у лінійному програмуванні?
- Побудуйте просту економіко-математичну модель. Запишіть до неї двоїсту. Дайте економічну інтерпретацію двоїстих оцінок.
- Які взаємоспряжені задачі називаються симетричними, а які — несиметричними? Чим вони відрізняються?
- Скільки змінних та обмежень має двоїста задача відповідно до прямої?
- Сформулюйте першу теорему двоїстості та дайте її економічне тлумачення.
- Сформулюйте другу теорему двоїстості та дайте її економічне тлумачення.
- Сформулюйте третю теорему двоїстості та дайте її економічне тлумачення.
- Сформулюйте правила побудови двоїстих задач.
- Як за розв’язком прямої задачі знайти розв’язок двоїстої?
- Запишіть усі можливі види прямих і двоїстих задач.
Приклади та завдання для самостійної роботи
До наведених нижче задач записати двоїсті задачі лінійного програмування. Розв’язати одну із задач симплекс-методом і визначити оптимальний план другої задачі, застосовуючи співвідношення першої теореми двоїстості.
Задача 3.1. mах z = –30x1 + 10x2;

Задача 3.2. min z = 4x1 + 3x2 + x3;
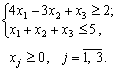
Задача 3.3. max z = 3x1 + 2x2 + 5x3;
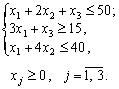
Created/Updated: 25.05.2018
 |
|