- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
2.8.8. Геометрична інтерпретація симплексного методу
Геометричну інтерпретацію симплексного методу можна подати двома різними способами. В одному разі ілюструється зміна базису, яка здійснюється вибором векторів, які включаються до базису та виключаються з нього. В другому, простішому та наочному випадку, процес симплексного методу інтерпретується як послідовний рух через сусідні кутові точки багатогранника розв’язків, що пов’язано зі збільшенням (зменшенням) значення цільової функції.
Дві кутові точки назвемо сусідніми, якщо вони розташовані на одному ребрі багатогранника.
Допустимо, що розглядається задача на відшукання максимального значення лінійної функції 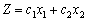 і маємо певний багатокутник її розв’язків (рис. 2.18).
і маємо певний багатокутник її розв’язків (рис. 2.18).

Допустимо, що початковий опорний план відповідає кутовій точці А. Тоді наступний крок симплексного методу приведе до точки Q, (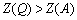 ), а в результаті ще однієї ітерації — до точки K, де лінійна функція набуває максимального значення. Проте, якщо початковим опорним планом буде точка В, то включення вектора до базису за критерієм
), а в результаті ще однієї ітерації — до точки K, де лінійна функція набуває максимального значення. Проте, якщо початковим опорним планом буде точка В, то включення вектора до базису за критерієм 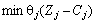 приводить до того, що пряма
приводить до того, що пряма  проходитиме через точку С і алгоритм симплексного методу приведе до точок С, D, E, F, K, тобто для отримання оптимального плану необхідно буде виконати ще чотири ітерації.
проходитиме через точку С і алгоритм симплексного методу приведе до точок С, D, E, F, K, тобто для отримання оптимального плану необхідно буде виконати ще чотири ітерації.
Отже, очевидно, що застосування симплексного методу не дає змоги одразу перейти від опорного плану (точки В) до оптимального (точки К). Фактично розв’язок отримують, рухаючись вздовж межі (ребер) простору розв’язків, причому не завжди такий шлях буде найкоротшим. Кількість ітерацій за реалізації симплексного алгоритму визначається вибором початкового опорного плану та кількістю кутових точок, що траплятимуться на шляху прямої 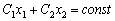 .
.
Created/Updated: 25.05.2018
 |
|